Why the earth can’t be the center of mass of the universe.
by Gary Hoge
In my article, As the Universe Turns, I refuted the claim made by geocentrists like Robert Sungenis that the earth sits at the exact center of mass of the universe. Mr. Sungenis read my article, and provided a rebuttal. This is my response to his rebuttal. My words are in normal font, and Mr. Sungenis’ are bold.
[F]or all his criticism of geocentrism (and me personally) he has written in the last two years, it is now apparent that he never considered the center of mass argument — the most important feature of the whole debate.
Mr. Sungenis is right, I never considered the “center of mass argument”. There are two reasons for that. One is that all of my previous critiques of geocentrism have been aimed at proving that the earth rotates on its axis, not that it orbits the sun. The “center of mass argument” is irrelevant to the question of whether the earth rotates. The second reason I never considered the “center of mass argument” before is that I had never heard of the “center of mass argument” before.
I find that revelation quite startling in light of the fact that Mr. Hoge has long-claimed to be a qualified critic of the geocentric issue, touting his employment as an “orbital mechanic” as one of his many qualifications.
I think Mr. Sungenis has me confused with someone else. I have never been employed as an “orbital mechanic,” nor have I claimed to be a qualified critic of the geocentric issue, or to have “many qualifications” in this field. My only qualification, aside from a life-long interest in astronomy, is a degree in Engineering Science and Mechanics, toward which I took courses in, among other things, physics, structural mechanics, and dynamics of rigid bodies. That probably makes me better qualified in this field than Mr. Sungenis, who, if memory serves, does not have a degree in any scientific field, but it hardly makes me an expert.
How good of a scientist can Mr. Hoge be if he has to be educated by his opponent to one of the most basic facts of science in regards to geocentrism?
Sorry, but they didn’t offer a course in geocentrism in the College of Engineering at Virginia Tech when I was there.
And in the process, Mr. Hoge has not admitted his shortsightedness to his audience, but instead congratulates me on what he considers new evidence in my favor. This is not just some minor mistake on Mr. Hoge’s part. It is a glaring omission that he has tried to address only this past week.
Actually, it is neither a mistake nor an omission. It’s simply an argument I hadn’t heard before. Once I read it, I thought about it. Then I asked Mr. Sungenis a few questions about it, to make sure I understood his position. Then I thought about it some more, and realized it wouldn’t work. Then I wrote a critique of it. I leave it to you, gentle reader, to decide whether there’s anything in that sequence of events that should be “startling” to Mr. Sungenis, or that undermines my credibility.
It will become apparent when we read Mr. Hoge’s hastily created apologetic that he has actually not thought out a lot of the issues involved, and he makes up the rules as he goes along.
Again, I’ll leave it to you, gentle reader, to be the judge of that.
In the end, however, we will see that Mr. Hoge’s admission that Earth could be the center of mass of the universe will entirely refute his objections to geocentrism, and this debate will be over.
Only if you stop reading my argument in the middle of it. I did say that if the geocentric conception of the universe were correct, the earth could, from time to time, be at the center of mass, but I went on to say that it couldn’t stay there for long. I also showed that if the center of mass of the universe is as close to the sun as the earth is, that point would not be a point of gravitational equilibrium, and therefore, no planet could remain stationary at that point.
After I explained how, in a geocentric world, the center of mass of the universe might momentarily coincide with the earth, Mr. Sungenis said:
Notice Mr. Hoge has admitted that, even from his critical perspective, it is indeed possible for the earth to be the center of mass of the universe. That position is quite different from what Mr. Hoge was admitting just two years ago. The reason, of course, is that two years ago Mr. Hoge never thought about connenction the principle of the “center of mass” to geocentrism.
Yes, two years ago I had not considered the “center of mass argument.” I have now considered it, and concluded that it doesn’t support geocentrism, even if the center of mass of the universe is right where Mr. Sungenis says it is. The reason he thinks this argument works is because he erroneously thinks the “center of mass” is the point at which all the gravitational forces cancel out. It isn’t. Therefore, it doesn’t matter whether the center of mass of the universe lies out where the earth is. The fact remains that it would be impossible for an object to remain stationary at a point that close to the sun. The object would either have to move fast enough to orbit the sun, or it would fall into it.
According to his prior critiques, it was impossible to consider the earth in the center of the universe, since, as he claimed, it would be “against the laws of Newton.” But it is obvious that Mr. Hoge did not contemplate the laws of Newton as well as he should have before he levied his critiques against geocentrism.
I never said any such thing. My prior critiques had nothing to do with whether the earth was the center of the universe, or even whether the earth orbits the sun. My prior critiques only addressed the question of whether the earth rotates on its axis. I demonstrated that the complex motion of several geosynchronous satellites is only explicable if the earth does in fact rotate.
Apparently, Mr. Hoge had never thought about the earth being the center of mass of a spherical distribution of stars before I suggested it to him.
That’s true. But it didn’t take much thought to realize that in order for such a thing to be possible, the mass distribution in this hypothetical “sphere of stars” must be slightly heavier in the direction opposite the sun, in order to counterbalance the mass of the sun and skew the center of mass out to the earth. But the problem is, the sun doesn’t stay put. It moves relative to the sphere of stars. Over the course of a year, it makes a complete circle of the sky. So, even if the mass distribution of the sphere of stars were heavier in one direction, the sun wouldn’t stay on the opposite side of the earth from that direction. Six months later it would be on the same side of the earth as the “heavier” side of the sphere of stars, and that would skew the center of mass back toward the sun.
Does Mr. Hoge really think that geocentrists “fail to take into account the fact that the universe is in a constant state of motion”?
Apparently so, since Mr. Sungenis makes no attempt to explain how the center of mass can stay put when the heavy objects in the system, especially the sun, move. That’s the question he must answer: If the sphere of stars is heavier on one side, in order to counterbalance the mass of the sun, how does the center of mass remain at the earth when the sun moves over to the “heavy” side of the sphere of stars?
Does he really think that we would advance the Newtonian phenomenon concerning the “center of mass” and then forget the Newtonian laws of gravity and inertia?
I don’t see why not. Mr. Sungenis advanced the Newtonian phenomenon concerning the “center of mass” and then apparently forgot – or never knew in the first place – that this isn’t the same thing as the Newtonian phenomenon of the “point of gravitational equilibrium.”
I find it interesting how Mr. Hoge tries to make it appear as if the geocentrists have failed to consider something, when, in fact, it was Mr. Hoge who failed to consider the argument concerning the center of mass.
Even if I had been aware of that argument, it was irrelevant to the question of whether the earth rotates on its axis, which was the entire thrust of my earlier critiques of geocentrism.
Obviously, it is Mr. Hoge’s desire to make geocentrists look like ignoramuses rather than admit his own mistakes.
How is not addressing the center of mass argument until now a “mistake” on my part? Did Mr. Sungenis ever mention this argument to me before? No, he did not. Is it prominently advanced on geocentrists’ websites? No, it is not. I did a Google® search using terms like “geocentricity,” “geocentric,” “geocentrism,” “center of mass,” and “center of gravity,” and found nothing relevant. If this is, as Mr. Sungenis says, “the most important feature of the whole debate,” the geocentrists have hidden it well.
And just so you know, I have no desire to make geocentrists look like ignoramuses. If their arguments sometimes leave people with that impression, that isn’t my fault.
[A]ccording to Mr. Hoge, if the celestial bodies are put in the proper place, it IS possible for the earth to be the center of mass, and consequently, geocentrism is possible. That, ladies and gentlemen, destroys Mr. Hoge’s scientific objections to geocentrism. He obviously won’t admit that to you, so I am pointing it out.
Nice try, but if you read the rest of my argument, what I said was if the celestial bodies are put in the proper place, and stay there, the earth could be at the center of mass of the universe. But that isn’t the case. Further, even if it were the case, geocentrism still does not appear to be possible, because a point in space that close to the sun, even if it were the center of mass of the universe, would not be a point of gravitational equilibrium.
Second, just what does Mr. Hoge mean by “So, if the earth ever were at the center of mass of the universe, even a geocentric universe, it wouldn’t be there for long”? Is this now a contest of duration rather than mechanics?
I mean simply that if the universe looks like geocentrists say it does – a sphere of stars surrounding our solar system – it might sometimes happen that the center of mass of that system would momentarily coincide with the earth. But because the masses in that system are constantly moving relative to each other, their combined center of mass must also move, so most of the time, the earth would not be at the center of mass. And again, even if it were, it must still either orbit the sun or fall into it.
I think Mr. Hoge has realized there is no way, based on Newtonian mechanics, to deny that the earth could be the center of mass of the universe. So now he must attack this new problem from a new angle. Thus the new apologetic is “duration.” But as we will see, that will also fail.
Duration is part of the problem. Geocentrism requires that the earth be the permanent center of the universe, but I don’t see how that’s possible if the masses in the universe are moving relative to each other, which they are. The much bigger problem, though, is gravity. The earth is simply too close to the sun to just sit there. It must either orbit the sun or fall into it, as I demonstrated.
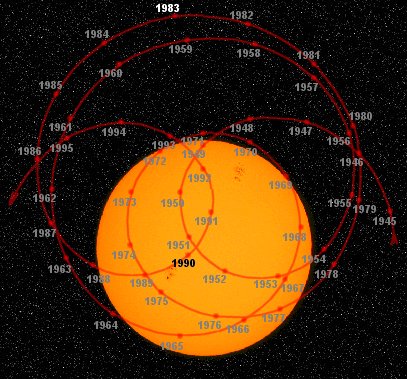
Next, I introduced the figure shown on the left. It shows the location of the solar system’s center of mass for each year between 1945 and 1995. The point of the figure was to illustrate the fact that the center of mass of a moving system will always be moving, too. As you can see, over a fifty-year period, the complex motion of the heavy outer planets, especially Jupiter, profoundly affects the location of the solar system’s center of mass. In 1983, for example, the center of mass was located a considerable distance from the center of the sun. That’s because in that year, all of the outer planets – Jupiter, Saturn, Uranus and Neptune – were on the same side of the sun, putting almost all of the solar system’s planetary weight on one side of the sun, and thus skewing the center of mass away from the sun. But in 1990, the center of mass of the solar system almost coincided with the center of the sun. That’s because in that year, Jupiter, which is heavier than all the other planets combined, was on the opposite side of the sun from Saturn, Uranus and Neptune. Thus, these large planets tended to balance each other out, and leave the center of mass near the center of the sun.
Mr. Hoge’s diagram of “The solar system’s center of mass 1945-1995″ is merely a mathematical model of what the center of mass for the solar system must be if the sun were at the center with all the planets revolving around it, and there was no consideration given to the gravity of the billions of stars in the universe.
Why would we consider the gravity of the stars? Gravity has nothing to do with center of mass. Unfortunately, it’s clear that Mr. Sungenis does not understand this, because throughout his rebuttal he speaks of gravity affecting the center of mass. It doesn’t. Only mass and distance affect the location of the center of mass.
In other words, scientists do not travel to the sun and planets and measure the center of mass with a yardstick. The heliocentric scientists simply use Newtonian laws of physics to plot out on a computer graph what they think is the movement of the center of mass. They may be close or far off, since it is very hard to calculate the center of mass with three moving bodies, let alone ten moving bodies. The point remains, however, that in the isolated sun/planet system, Mr. Hoge’s diagram is what the Newtonian laws will produce. And I agree: with nine planets revolving around the sun and no other counterbalancing forces, you will end up with a diagram very similar to the one Mr. Hoge has given us.
That being the case, my point is made, because the only possible “counterbalancing forces” (actually, counterbalancing masses) are the “sphere of stars”. But the sphere of stars would have to change its mass distribution constantly in order to precisely counterbalance the constantly-changing mass distribution of the moving planets. But the stars remain fixed relative to each other. We always see the same stars in the same place, forming the same constellations, year in and year out. Their masses don’t rearrange themselves in order to compensate for the motion of the planets. Therefore, even if we factor in the stars, the center of mass of the system is going to move just as the figure shows, even if the center isn’t located that close to the sun.
But how does Mr. Hoge know this is the same for the geocentric system? He doesn’t. He has no way of knowing if there will be a movement of the center of mass in the geocentric system.
Actually, I do, as I just explained. Even if Mr. Sungenis is right that if you factor in the masses of the billions of stars in the universe, the center of mass of the whole system would be near the earth, it doesn’t matter. As the figure shows, the motion of the nearby planets profoundly effects the location of the center of mass. In order to counteract that effect and to keep the center of mass stationary, the stars would have to move in complex ways, always precisely counterbalancing the motion of the planets. But the stars don’t move at all relative to each other. In a geocentric universe, the shell of stars rotates around the earth once each day, but its mass distribution never changes. Therefore, there’s no way it can counteract the motion of the planets and prevent the yearly motion of the center of mass.
If you’ve read Mr. Hoge’s previous arguments, he never considers the gravity of the stars and galaxies in his calculations. He keeps insisting that they are “too far away” to be of any consequence.
Clearly, Mr. Sungenis does not understand the concept of “center of mass,” which he himself introduced to the discussion. If you read my article, you know that the center of mass is simply the “balance point” of an object, or a group of objects. If you consider a system having only two objects, and if you think of the center of mass as the balance point between those two objects, it becomes clear that the farther away one of the objects is, the lighter it needs to be to “balance” the other object. That’s why the stars, because they are so far away, could easily counterbalance the nearby sun and planets.
But gravity, which Mr. Sungenis erroneously equates to center of mass, is a different matter entirely. With gravity, the farther away you go, the weaker the gravitational attraction becomes. In fact, it becomes weaker exponentially. Now, remember that my previous arguments concerned the motion of artificial satellites. The nearest star is so far away that, if it were the same size as the sun, it would exert about 0.0000000002 ounces of force on a typical satellite. That’s about 228,000 times less than the weight of a single snowflake.
Also, when you consider the fact that the sky is full of stars, you realize that for every star on one side of the satellite exerting its unmeasurably-small gravitational pull, there’s another star on the other side of the satellite pulling the other direction and cancelling it out. That’s why I “never consider[ed] the gravity of the stars and galaxies in [my] calculations” regarding earth-orbiting satellites. The stars are simply too far away, and too evenly distributed, to have any gravitational effect on their motion.
Unfortunately for him, you can’t do proper physics without considering the stars. Newton’s “swirling bucket of water” experiment will show that any system that does not take into account the force from the stars will be totally inadequate. In light of that, Mr. Hoge could not even begin to calculate the counterbalancing gravitational force from the stars against any potential of the shifting of the center of mass. In essence, his own logic silences his objection.
Again, “counterbalancing gravitational force” has nothing to do with shifting the center of mass. They are completely unrelated concepts.
Be that as it may, Mr. Hoge’s only recourse is to posit that God Himself would not be able to figure out what would be the proper balance of forces in the starry universe to keep the earth as its unvarying center of mass.
Overlooking, yet again, Mr. Sungenis’ erroneous equating of “balance of forces” with “center of mass,” my argument has never been about what God could have done, it’s about what He did. Obviously, God could have balanced the masses (not “forces”) in the starry universe to keep the earth as its unvarying center of mass, but He didn’t. Get out your telescope and you can see for yourself that God didn’t put any moving masses out there that can counterbalance the motion of the planets. He also could have made the earth sit at a point of gravitational equilibrium (which is not the same thing as “center of mass”) so that it wouldn’t plunge into the sun, but again, He didn’t. Look and see: there aren’t any masses out there that are sufficient to counterbalance the gravitational attraction of the sun. Instead, God gave the earth enough velocity to orbit the sun at a distance conducive to sustaining the life of His creatures.
Mr. Hoge is in quite a bind, since he has already admitted that, in principle, the earth could indeed be the center of mass. Once that admission is made, the only thing now needed to prove our case is for someone to balance out all the forces in the universe so that the earth could remain the center of mass.
Obviously, Mr. Sungenis thinks that the center of mass is the point at which “all the forces in the universe” balance out, and that’s why he thinks his argument works. But it doesn’t work because the center of mass is not the point at which all the forces balance out. It’s simply the center point of the mass distribution. If one of those masses is large and close to the center of mass – as the sun is both large and close to the earth – the center of mass will not be a point of gravitational equilibrium because the gravitational attraction of that large mass will cause there to be a net force on any object located at the center of mass. Thus, even if the center of mass of the universe were located 93 million miles from the sun (where the earth is), that location is so close to the sun that its gravitational attraction would cause there to be a powerful net force on the earth.
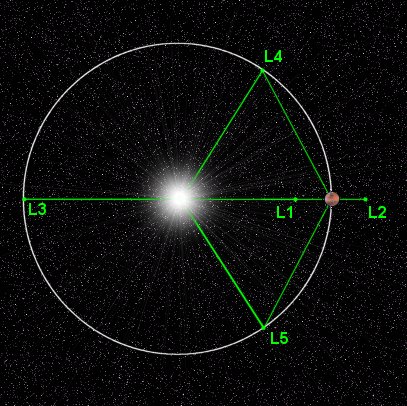
In a planetary system, there is only one center of mass, but there are many points at which the gravitational forces balance out. These are called “Lagrange points.” Every orbiting object of significant mass, i.e., a planet or a moon, has five Lagrange points associated with it, and this fact can be used to prove, yet again, that the earth is an orbiting object.
The figure at left shows the five Lagrange points associated with Mars. Lagrange point 1 (L1) is simply the point between the sun and Mars where their respective gravitational pulls balance each other. This point will exist between any two massive objects, regardless of whether one is orbiting the other or not. But Lagrange point 2 (L2) only exists on the far side of an object that is orbiting another object. The reason for this is easy to understand, but takes a few minutes to explain.
Orbital laws are such that objects in higher orbits move more slowly than objects in lower orbits. So, planets that are farther from the sun orbit more slowly than planets that are closer. That’s because the farther out you get, the weaker the gravitational pull from the sun will be, and the less velocity you’ll need to remain in orbit. You would expect, then, that an object located farther out than Mars would orbit more slowly than Mars, because it would feel less of a gravitational tug from the sun than Mars does. Ordinarily, you’d be right. But if the object is near Mars, it’s not only going to feel a tug from the sun, it’s going to feel a tug from Mars, too. That’s going to make it orbit faster. The L2 point is the point at which the object feels the same gravitational tug from the sun and Mars that Mars itself feels from just the sun. Therefore, because the object experiences the same gravitational attraction that Mars experiences, it will orbit the sun in 687 days, just like Mars does. So, the object will remain stationary with respect to Mars.
You can see, then, that L2 is a point of equilibrium for an object near Mars. You can also see that if Mars weren’t orbiting the sun, there would be no L2 point. Therefore, if an L2 point exists on the far side of the earth, too, then that would prove that the earth, too, is orbiting the sun.
Until recent years, there was no way to prove whether earth had an L2 point. But in 2001, NASA, believing that the earth is in orbit around the sun, attempted to place the Wilkinson Microwave Anisotropy Probe (WMAP) at the earth’s L2 point, so that the probe would orbit the sun in sync with the earth. If the earth were not, in fact, orbiting the sun, this attempt would have failed, because there would be no L2 point associated with the earth. The probe, then, would have orbited the earth every 213 days, instead of orbiting the sun every 365 days. But the mission succeeded. WMAP stays put1 right where NASA expected it to, thus proving that the earth has an L2 point, and thereby proving, yet again, that the earth orbits the sun.
But because Mr. Hoge does not have the ability to figure it out, he hastily concludes that it is impossible to have the earth remain the center of mass.
It is impossible for the earth to remain the center of mass, because of the motion of the sun and the planets, and the absence of any mechanism of precisely countering that motion, as I’ve already explained. But it is also irrelevant whether the earth is the center of mass. Even if it were, and even if it remained so, there is a strong net gravitational force at that location because of the nearby, massive sun. Therefore, it would be impossible for the earth to remain motionless at that point.
Do you think that if God was smart enough to place the Earth as the center of mass, He was also smart enough to keep it from shifting?
Yes, and I also think that God was smart enough to know that the center of mass is not the point at which all the forces in the universe balance out, thus enabling a planet at that point to remain at rest. God probably also would have realized that even if such an equilibrium point existed, it would be an unstable equilibrium. Of course, God could have created a universe in which a point of stable equilibrium existed at the center of mass, but that would require different physical laws than the ones He did in fact create. Instead, God created the laws of gravitation that we all know and love, and He placed the earth in such proximity to the sun that the earth must orbit the sun in order to avoid falling into it, just like all the other planets.
Yes, God, with his infinite mind, has already done so. He chose all the right masses, positions, angles and distances; and according to Scripture, the Fathers, and our seventeenth century magisterium, He calculated it with such precision that the earth remains in the center of the universe, and is its center of mass, without deviation.
I have already shown that this is not physically possible, given the masses in the universe and their relative motions. In order to be credible, Mr. Sungenis will have to specify which masses are able to counterbalance the moving masses of the planets and thus enable the center of mass of the system to remain fixed at the earth. He will also have to specify which masses are able to counterbalance the gravitational attraction of the sun, and, to a much lesser extent, the gravitational attractions of the nearby planets, such that the fixed center of mass also becomes a point of gravitation equilibrium. And finally, he will have to explain how this equilibrium, which would be inherently unstable, becomes stable.
But apparently Mr. Hoge thinks that although God can call things into being ex nihilo, He doesn’t have the intelligence to calculate all such forces in the universe in order to keep Earth as the center of mass.
Again, this is not about what God is able to do; it’s about what He has done. He created the laws of gravitation and motion; He created the sun, moon, planets and stars; He put them in the sky and set them in motion. Given the parameters He Himself established, it is not physically possible for the earth to be permanently at the center of mass, nor is it possible for the earth to be at a point of gravitational equilibrium.
Here we see the perennial problem with Mr. Hoge’s whole approach to this issue, and why he simply cannot understand or accept the geocentric system. We have billions upon billions of stars in the universe, many much greater in size than the sun, they swirl around us every night like a big ball, but somehow Mr. Hoge thinks that all those stars simply have no effect upon our sun and earth.
I didn’t say they had “no effect” upon our sun and earth. I said that they are simply too far away to exert enough gravitational pull to counterbalance the gravitational pull of the sun, which is what would have to happen in order for the earth to be sitting at a point of gravitational equilibrium.
Yet, as a heliocentrist, he must believe that the gravity of a single galaxy, our Milky Way, is so strong that the sun must travel 500,000 mph to escape being pulled into its core.
I’m sorry, but Mr. Sungenis can’t have it both ways. Either our galaxy is one galaxy among thousands of other galaxies, and our solar system is on the fringe of that galaxy, orbiting the galaxy’s center of mass, or the whole universe is just a relatively-thin shell of stars orbiting the earth every day. It is the latter system that Mr. Sungenis is defending, and that I am critiquing.
So if just one galaxy’s gravity so strongly affects our solar system, how can Mr. Hoge say there is “nothing in the whole universe that can exert enough force to rival the gravitational pull from the sun”?
Because there isn’t. The force of gravity exerted on the earth by the stars is negligible compared to the force of gravity exerted on the earth by the sun. That’s because the sun is so much closer to the earth than the other stars are, and that’s why the earth orbits the sun and not the center of the Milky Way galaxy.
Now, just add the gravitational force of billions of galaxies to the gravitational force of the Milky Way, and you have a good idea of how powerful are the forces in the universe that affect our little Sun and Earth. If you don’t believe that, then go ask Newton, Mach and Einstein about Newton’s bucket.
How powerful is the gravitational attraction of a galaxy? That depends on how far away the galaxy is. I don’t know how far away Mr. Sungenis thinks the galaxies are, so I can’t address that. However, there are two problems that Mr. Sungenis still has not accounted for. One is the fact that the galaxies appear to be more-or-less evenly distributed around the sky. Therefore, if the earth is at the center of the universe, the gravitational attractions of the various galaxies are going to cancel out. In order to counterbalance the gravitational attraction of the sun, there would have to be a huge imbalance in the number of galaxies on the side of the sky opposite the sun.
But that leads us to the second problem: the sun moves. Even if the universe were significantly imbalanced in a certain direction, the sun would not always be located on the opposite side of the earth from that direction. Half of the time, the sun would be on the same side. Then what would counterbalance the gravitational pull of the sun?
For that matter, Mr. Hoge doesn’t even know what gravity is. He keeps talking about the “gravitational pull from the sun” but he doesn’t know it is coming from the sun, or if it is a pull, a push, an electrical attraction or angels pushing things together. He doesn’t know if it is the sun alone, the sun mixed with the stars, or any other combination of forces.
I don’t need to know what gravity is, I just need to be able to predict its behavior, which, thanks to Newton’s laws, I can.
The only thing Mr. Hoge knows is that the force of gravity in a given locale is inversely proportional to the square of the distance . . .
That’s all I need to know in order to calculate the force of gravity at a given locale.
. . . but that is true with any force of nature, e.g., light, sound, waves, density, etc.
Density? How does density obey the inverse square law?
There is no mystery to the inverse square law. It is just a geometric fact.
Yes, and that fact makes geocentrism impossible, as I’ve shown.
But it doesn’t tell you what is actually producing the forces. The only thing Mr. Hoge knows is that there are forces out there, but he can’t prove where they originate. What I am telling him is that it is not just the sun, but the whole universe that is involved, and modern physics supports that conclusion.
As Mr. Sungenis said, there’s no mystery to the inverse square law. That law tells me that the farther away an object is, the less its gravitational attraction will effect the earth. So, knowing the mass of the sun (1.989 x 1030 kg) and the earth (3.3 x 1023 kg), and knowing the distance between them (1.496 x 1011 m), I can calculate the force (1.956 x 1021 N) the sun will exert on the earth. Therefore, knowing that the nearest star is at least 4 light years away, I can easily calculate that at that distance it would take almost a whole galaxy to exert a sufficient counterforce, and there isn’t a galaxy 4 light years away. The nearest one is 2 million light years away.
Mr. Sungenis might reply that in a geocentric universe, the galaxies are much closer than we think. But again, the fact that the sun moves relative to the stars, and thus relative to any potential counterbalancing mass, makes a permanent counterbalance impossible.
Mr. Hoge keeps showing diagrams of two bodies, as if the issue of the “center of mass” is very simple. It is not. When we add in three or more bodies, the calculations are astronomically difficult.
That’s true, but the point of my diagrams is to illustrate the concept, not to prove that the calculations are easy when multiple bodies are involved.
In this next paragraph, instead of noting, yet again, Mr. Sungenis’ erroneous use of the word “forces,” I’m just going to correct the text for him:
When you add in ALL the forces masses of the universe, then it becomes quite impossible to calculate how the forces masses are distributed. Mr. Hoge has no idea what all those forces masses are, yet he insists that Earth can’t be the center of mass, at least for long. This is nothing but pure desperation on his part.
It’s true, I have no idea where the center of mass of the universe really is. But there are a few things I do know:
- The mass distribution of the solar system is constantly changing as the various planets move in their orbits around the sun.
- That redistribution of masses will necessarily cause the combined center of mass of the planetary system to shift.
- Assuming that the center of mass of the universe is located somewhere in our solar system, it, too, will shift unless the other objects in the universe (stars, galaxies, etc.) move in such a way as to counterbalance the motion of the planets.
- The stars do not move. They are always in the same place, making the same constellations, year in and year out. Yes, I know that in a geocentric universe, the stars move around the earth once each day. But each day they’re right back where they started the day before. The motion of the planets takes place over a period of years. In order to counterbalance that motion, the stars would have to realign themselves over a period of years, thus forming new constellations. That doesn’t happen.
Therefore, the center of mass of the universe cannot be stationary. In my article I said: “the amount of mass it would take to counteract the gravitational pull from the sun increases exponentially as you move away from the earth. By the time you get out to the edge of the solar system, it would take over 1,500 suns to do it! By the time you get to the nearest star, over four light years away, it would take more than the mass of the whole galaxy. In fact, it would take more than the mass of a trillion galaxies.”
Which is it, Mr. Hoge? Does it take a “whole galaxy” at a distance of four light years, or does it take “a trillion galaxies”? There is quite a difference, you know. My guess is that Mr. Hoge didn’t even begin to calculate what the force of more than one galaxy would be, let alone a trillion. Until he does, we really aren’t interested in his speculations.
Actually, I did do the math, but it turns out I made an error in one of my calculations that gave me an answer that was wrong by several orders of magnitude. I caught the error today when I double-checked the calculations. It turns out that at a distance of four light years, it wouldn’t take over a trillion galaxies to compensate for the gravitational attraction of the sun, it would take “only” about 71 billion stars, which is less than one galaxy.
I regret the error, and have corrected it in my article. Fortunately, though, the error affected the number, but not the point I was trying to make. Whether it would take billions of galaxies or billions of stars, the result is the same: there simply isn’t that much mass all clustered together only four light years away at a point opposite the sun. And, once again, even if there were, the sun moves relative to the stars, and that makes it impossible for the stars to be a permanent counterbalance to the sun.
From the geocentric perspective, it is clear why God put so many stars in the universe, since they are all needed to create the necessary forces to keep our sun-earth system in balance
I have painstakingly explained why the observed motion of the stars – even in a geocentric universe – is insufficient to keep our planetary system in balance. Mr. Sungenis has made no attempt to answer my arguments, or to show that they are deficient, or to propose a solution to the problems I raised. His only answer is to ignore the evidence and assert that everything somehow balances anyway. That is a statement of faith, not a rebuttal.
I think it is clear that Mr. Hoge just went on a fishing expedition to answer a series of problems he previously never considered. Because of the evidence brought before him, he has had to admit that a geocentric model based on the Earth being the center of mass is, in his own words, “…the most plausible explanation of geocentrism I’ve yet heard.” And indeed it is.
An obvious objection to geocentrism is that the earth isn’t nearly massive enough to cause the whole universe to orbit it. But it is true that planetary systems orbit their center of mass. Therefore, the idea that the universe orbits the earth because the earth sits at the center of mass was the most plausible explanation of geocentrism I had yet heard. Unfortunately, it didn’t take much thought to realize it wouldn’t work.
Admitting this, Mr. Hoge was then forced to come up with some explanation why the “center of mass” argument would not work, that is, if he intended on maintaining that heliocentrism is the only true system. His only option was to hypothesize that if Earth was the center of mass it would necessarily shift, and thus the Earth would not always be the center of mass.
You’ll notice that Mr. Sungenis made no serious attempt to answer this objection to his theory; he simply asserted that the universe moves in such a way as to make everything balance. But I have repeatedly pointed out that there is no observed motion in the universe that corresponds to the motion of the planets. If the universe is geocentric and the earth doesn’t rotate, then the shell of stars spins around the earth once each day, but the distribution of stars in that shell never changes. It takes Jupiter 12 years to go around the sun. What is there in the universe that moves in such a way as to counterbalance the motion of Jupiter over a 12-year period?
But Mr. Hoge hasn’t even begun to prove that the Earth, as the center of mass, would shift, for he simply hasn’t made all the calculations necessary to arrive at such a conclusion. Mr. Hoge simply cannot superimpose the calculations he makes from his limited sun-planet system onto a geocentric system, and then demand that it follow his directions.
It’s more a matter of observation than of calculation. I observe that the planets orbit the sun, and that each of the planets does so at a different speed. I know, as a basic principle of physics, that such a redistribution of planetary masses would cause the center of mass of the solar system to shift constantly unless there were some other masses out there that moved in such a away as to precisely compensate for the motion of the planets. I observe that there are no other masses that move in such a way. The stars themselves are fixed relative to each other. They are not constantly moving around, forming new constellations. Therefore, I can affirm that the center of mass of the whole system must move as the planets move.
The fact is, unless Mr. Hoge wants to add up all the forces of all the stars in the universe and counterbalance them against the sun and planets, then he is never going to have the evidence to deny the Earth as the invariable center of mass for the universe.
On the contrary, I have all the evidence I need. The planets move relative to each other, and the stars do not. That fact alone sinks the “center of mass argument.” Unless Mr. Sungenis can tell me what moves to counteract the mass of Jupiter as it goes around the sun every 12 years, his geocentric theory falls apart.
We’ve already seen by his reference to “a trillion galaxies” that Mr. Hoge likes to throw around mental images without actually doing the calculations required of him. This kind of explanation may convince the folks who don’t know any better, but for those of us who know better it is nothing more than a desperate attempt to save face for himself.
I leave it to you, gentle reader, to decide which of us is in a desperate situation. I presented two reasons that the center of mass argument can’t work. First, the center of mass is constantly moving as the planets in the system move. In a geocentric universe the shell of stars does nothing but spin around the earth once each day. Its many masses do not move relative to each other, and so the composition of the shell does not change over time. Therefore, it cannot compensate for the motion of Jupiter, or the motion of Saturn, or the motion of Uranus, or the motion of Neptune, etc. These planets take many years to go around the sun, and over time, the closer planets “lap” the ones farther out, because the closer planets go around the sun faster. This results in a complex and constantly shifting balance of masses. A fixed shell of stars that spins around the earth each day can’t compensate for that motion, because it doesn’t redistribute its mass over a multi-year period. If Mr. Sungenis disagrees, he should explain his reasoning.
Second, I showed that the earth, because of its proximity to the sun, does not occupy a position of equilibrium. Even if we assume that the universe is a thin shell of stars beginning about 4 light years away, and extending no more than 300 light years, those objects are simply too far away to counteract the gravitational attraction of the sun. And even if the universe were imbalanced in such a way that it were heavy enough on one side to counterbalance the sun’s gravity, the sun moves relative to the stars, so a permanent counterbalance is not possible. I notice that Mr. Sungenis didn’t even address this last point. I don’t blame him. It is fatal to his theory.
I want to thank Mr. Sungenis for replying to my article. If he would like to make a substantive reply to the two objections I raised to his theory, I would be glad to consider his arguments.